Diferencia de Fase o Desfase en CA

La diferencia de fase entre dos ondas es un tema muy importante por cubrir en el campo de la energía eléctrica alterna, ya que nos ayuda a describir la diferencia entre grados o radianes cuando dos o más cantidades alternas alcanzan su valor máximo o cero.

En los artículos anteriores a este tema sobre la corriente eléctrica alterna vimos que una forma de onda sinusoidal es una cantidad alterna que se puede presentar gráficamente en el dominio del tiempo a lo largo de un eje horizontal. También vimos que, como una cantidad alterna las ondas sinusoidales poseen un valor máximo positivo en el tiempo π/2, un valor máximo negativo en el tiempo 3π/2, y valores cero a lo largo de la línea base en 0, π, y 2π.

Sin embargo, no todas las formas de onda sinusoidales pasarán exactamente por el punto del eje cero al mismo tiempo, pero pueden “desplazarse” hacia la derecha o hacia la izquierda de 0° en algún valor en comparación con otra onda sinusoidal.

Interpretando la diferencia de fase 

Por ejemplo, comparar una forma de onda de voltaje con la de una forma de onda de corriente, se puede denotar fácilmente por el cambio angular o diferencia de fase entre las dos formas de onda sinusoidales. Cualquier onda sinusoidal que no pase por cero en t = 0, tiene un cambio de fase.

La diferencia de fase o cambio de fase de una forma de onda sinusoidal que se representa mediante el ángulo Φ (letra griega Phi), en grados o radianes que la forma de onda se ha desplazado desde un cierto punto de referencia a lo largo del eje horizontal. En otras palabras, el cambio de fase es la diferencia lateral entre dos o más formas de onda a lo largo de un eje común y las formas de onda sinusoidales de la misma frecuencia pueden tener una diferencia de fase.

La diferencia de fase (Φ) de una forma de onda alterna puede variar entre 0 y su periodo de tiempo máximo (T), de la forma de onda durante un ciclo completo y esto puede estar en cualquier lugar a lo largo del eje horizontal entre Φ = 0 a 2π (radianes) o también de Φ = 0 a 360° dependiendo de las unidades angulares utilizadas

La diferencia de fase también se puede expresar como un cambio de tiempo de t en segundos, que representa una función del periodo de tiempo, T por ejemplo, +10mS o -50uS pero generalmente es más común expresar la diferencia de fase como una medida angular.

Fórmula de diferencia de Fase

La ecuación para el valor instantáneo de una forma de onda sinusoidal de voltaje o corriente deberá modificarse para tener en cuenta el ángulo de fase de la forma de onda y se convierta en esta nueva expresión general

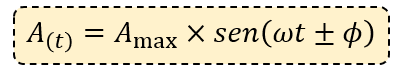
Dónde:

• A_m es la amplitud de la forma de onda.
• ωt   es la frecuencia angular de la forma de onda en radianes/seg.
• Φ (phi) : es el ángulo de fase en grados o radianes que la forma de onda se ha desplazado hacia la izquierda o hacia la derecha desde el punto de referencia.

¿Fase negativa a fase positiva?

Si la pendiente positiva de la forma de onda sinusoidal pasa por el eje horizontal “antes” de t = 0, entonces la forma de onda se ha desplazado hacia la izquierda, por lo que Φ > 0, y el ángulo de fase será de naturaleza positiva + Φ dando un ángulo de fase adelantado. En otras palabras, si aparece antes de 0° produciendo una rotación antihoraria del vector.

Del mismo modo, si la pendiente positiva de la forma de onda sinusoidal pasa a través del eje horizontal algún tiempo “después” de t = 0, entonces la forma de onda se ha desplazado hacia la derecha, por lo que Φ < 0, y el ángulo de fase será de naturaleza negativa – Φ , produciendo un ángulo de fase retrasado que aparece más tarde que 0° produciendo una rotación del vector en el sentido de las agujas del reloj.

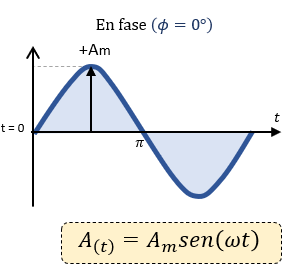
Forma de onda sinusoidal: “en fase”

En primer lugar, consideremos que dos cantidades alternas, como un voltaje, v y una corriente, tienen la misma frecuencia ƒ en Hertz. Como la frecuencia de las dos cantidades es la misma que la velocidad angular, ω también debe ser la misma. Entonces, en cualquier instante podemos decir que la fase del voltaje V, será la misma que la fase de la corriente, i .

Entonces, el ángulo de rotación dentro de un período de tiempo particular siempre será el mismo y la diferencia de fase entre las dos cantidades de v e i será por lo tanto cero y Φ = 0 . Como la frecuencia de la tensión, vy la corriente, i son iguales, ambas deben alcanzar sus valores máximos positivo, negativo y cero durante un ciclo completo al mismo tiempo (aunque sus amplitudes pueden ser diferentes). Entonces se dice que las dos cantidades alternas, v e i , están "en fase".

Diferencia de fase de una forma de onda sinusoidal

Para observar la diferencia de fase, es muy sencillo basándonos en el siguiente ejemplo (ver la imagen debajo), consideremos que el voltaje (v) y la corriente (i), tienen una diferencia de fase entre ellos de 30° o bien π/6 radianes. Como ambas cantidades alternas giran a la misma velocidad, es decir, tienen la misma frecuencia, esta diferencia de fase permanecerá constante durante todos los instantes de tiempo, de tal forma que la diferencia de fase será de 30° entre las dos cantidades, que se representa por Φ.

Es fácil notar que la forma de onda de voltaje comienza en cero a lo largo del eje horizontal, pero en ese mismo instante se puede apreciar que la forma de onda de corriente todavía tiene un valor negativo y no cruza este eje de referencia hasta 30° más tarde, es allí donde decimos que existe un diferencia de fase entre las dos formas de onda, o también podemos decir que están desfasadas por 30° o también se puede decir que la forma de onda de corriente está “retrasada” con respecto a la forma de onda de voltaje por el ángulo de fase Φ.

El ángulo de fase de una onda sinusoidal se puede utilizar para describir la relación de una onda sinusoidal con otra utilizando los términos "Adelanto" y "Retraso" para indicar la relación entre dos formas de onda sinusoidales de la misma frecuencia, trazadas en el mismo eje de referencia. En nuestro ejemplo anterior, las dos formas de onda están desfasadas en 30°. Así que podemos decir correctamente que i se retrasa v o podemos decir que v se adelanta i por 30° o dependiendo de cuál elijamos nuestra referencia

La relación entre las dos formas de onda y el ángulo de fase resultante se puede medir en cualquier lugar a lo largo del eje horizontal a través del cual pasa cada forma de onda con la "misma pendiente" en la dirección, ya sea positiva o negativa.

En los circuitos de alimentación de CA, esta capacidad para describir la relación entre una tensión y una onda sinusoidal de corriente dentro del mismo circuito es muy importante y constituye la base del análisis de circuitos de CA

La forma de onda del Coseno

Algo que es muy importante mencionar es que si una forma de onda se “desplaza” a la derecha o a la izquierda de 0° en comparación con otra onda sinusoidal, la expresión de esta forma de onda se convierte en A_m  sin(ωt ±  Φ). Pero si la forma de onda cruza el eje horizontal con una pendiente positiva de 90° o π/2 radianes antes de la forma de onda de referencia, la forma de onda se denomina Forma de onda Coseno y la expresión matemática se convierte en: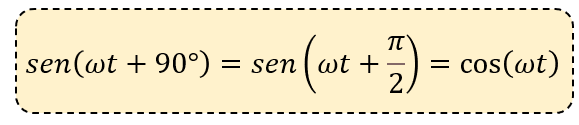

La onda coseno es tan importante como la onda sinusoidal en ingeniería. La onda coseno tiene la misma forma que su contraparte de onda sinusoidal, es decir, es una función sinusoidal, pero se desplaza +90° o cuarto completo en u período por delante.

Alternativamente, también podemos decir que una onda sinusoidal es una onda coseno que se ha desplazado en la otra dirección en -90 ^° . De cualquier manera, cuando se trata de ondas sinusoidales u ondas cosenoidales con un ángulo, siempre se aplicarán las siguientes reglas.

Relaciones de onda seno y coseno

Matemáticamente podemos observar ciertas comparaciones de formas de onda, es más común expresar su relación como un seno o un coseno con amplitudes positivas y esto se logra utilizando las siguientes reglas.

$\displaystyle \cos (\omega t+\phi )=sen(\omega t+\phi +90{}^\circ )$

$\displaystyle sen(\omega t+\phi )=sen(\omega t+\phi -90{}^\circ )$

Cuando se comparan dos formas de onda sinusoidales, es más común expresar su relación como un seno o un coseno con amplitudes positivas y esto se logra utilizando las siguientes identidades:

$\displaystyle sen(A\pm B)=sen(A)\cos (B)\pm \cos (A)sen(B)$

$\displaystyle \cos (A\pm B)=\cos (A)\cos (B)\pm sen(A)sen(B)$

Por lo tanto:

$\displaystyle -sen(\omega t)=sen(\omega t\pm 180{}^\circ )$

$\displaystyle -\cos (\omega t)=\cos (\omega t\pm 180{}^\circ )$

$\displaystyle \pm sen(\omega t)=\cos (\omega t\mp 180{}^\circ )$

$\displaystyle \pm \cos (\omega t)=sen(\omega t\pm 90{}^\circ )$

Al usar estas relaciones matemáticas, podemos convertir cualquier forma de onda sinusoidal con o sin una diferencia angular o de fase de una sinusoidal a una onda coseno o viceversa.