Fasores en Corriente Alterna: La Guía Definitiva

El tema de los fasores es muy importante dentro de la corriente eléctrica alterna, pues es clave comprender la representación gráfica de la relación de fase entre voltajes y corrientes. Generalmente, los fasores se definen en relación con un fasor de referencia que siempre apunta a la derecha (eje X).

Las formas de onda sinusoidales de la misma frecuencia pueden tener una diferencia de fase, que representa la diferencia angular entre ellas. Los términos “adelanto”, “retraso”, “en fase” y “fuera de fase” se usan para indicar la relación de una sinusoide con otra.

La expresión sinusoidal generalizada, dada como:

\[ A_{(t)} = A_{m}\sin(\omega t \pm \Phi) \]

...representa la sinusoide en el dominio del tiempo. Pero de esta forma, a veces es difícil visualizar la diferencia angular. Para superar esto, representamos las sinusoides en el dominio fasorial mediante diagramas fasoriales, usando el método del vector giratorio.

Básicamente, un vector giratorio o “Vector de fase”, es una línea escalada cuya longitud representa una cantidad de CA que tiene tanto magnitud (amplitud) como dirección (fase) y que se ha “congelado” en un instante de tiempo.

Se supone que los vectores pivotan en un extremo alrededor de un punto de origen. El extremo con flecha gira libremente en sentido contrario a las agujas del reloj a una velocidad angular (\(\omega\)). Esta rotación se considera positiva.

La fase de una cantidad alterna se puede representar mediante diagramas fasoriales. Por lo tanto, un fasor es una cantidad que tiene tanto “Magnitud” como “Dirección”.

Debemos recordar que los vectores obedecen la ley del paralelogramo, por lo que se pueden sumar. Los fasores, por otro lado, representan la forma matemática (Rectangular, Polar o Exponencial). Por ejemplo: \( Z = a + jb \). Generalmente, cuando se construye un diagrama fasorial, se asume la velocidad angular \(\omega\) en rad/s.

Diagramas Fasoriales para una forma de onda sinusoidal 🔄

A medida que el vector (color rojizo) gira en sentido contrario a las agujas del reloj, su punta (punto A) girará una revolución completa de 360° o \(2\pi\) radianes, representando un ciclo completo.

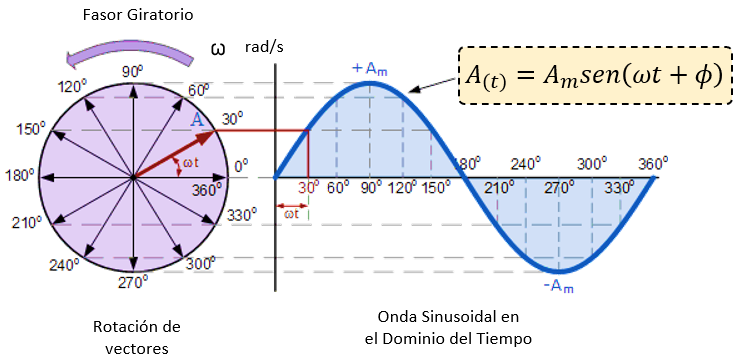
Si la longitud de su punta se transfiere a diferentes intervalos angulares en el tiempo, se dibuja una forma de onda sinusoidal. Cada posición en el eje horizontal indica el tiempo transcurrido desde \(t = 0\).

• Cuando el vector es horizontal, representa los ángulos 0°, 180° y 360°.
• Cuando el vector es vertical, representa el valor pico positivo (+\(A_m\)) a 90° o \(\pi/2\) y el valor pico negativo (-\(A_m\)) a 270° o \(3\pi/2\).

Entonces, un fasor representa un valor escalado de un vector giratorio "congelado" en un instante (en el ejemplo, a 30°).

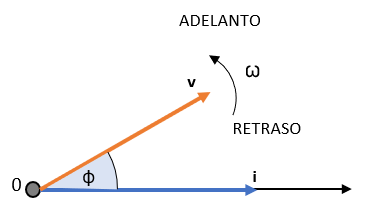
A veces necesitamos conocer la posición del fasor para comparar dos formas de onda, por ejemplo, voltaje y corriente. Si una segunda forma de onda comienza a la izquierda o derecha del punto cero, debemos tener en cuenta la diferencia de fase, \(\phi\).

La expresión matemática para estas dos cantidades será:

\[ {{v}_{{(t)}}}={{V}_{m}}\sin(\omega t) \]\[ {{i}_{{(t)}}}={{I}_{m}}\sin(\omega t-\phi ) \]

La corriente i está atrasada con respecto al voltaje v por el ángulo \(\phi\) (en el ejemplo, 30°). La diferencia entre los dos fasores es el ángulo \(\phi\).

Diagrama fasorial de una forma de onda sinusoidal

El diagrama fasorial se dibuja correspondiente al tiempo cero (\( t = 0 \)) en el eje horizontal. Las longitudes son proporcionales a los valores de V e I. El fasor de corriente se atrasa del fasor de voltaje en el ángulo \(\phi\), ya que giran en sentido antihorario.

Sin embargo, si las formas de onda se congelan en \(t = 30^\circ\), el diagrama se vería como el de la derecha. Como la corriente ahora cruza el eje cero, podríamos usarla como nueva referencia y decir que el voltaje "adelanta" a la corriente por el ángulo \(\phi\). Siempre se designa un fasor de referencia.

¿Cómo se suman los fasores?

Si están "en fase", es una simple suma algebraica (50V + 25V = 75V). Si no están en fase, se debe tener en cuenta el ángulo y usar diagramas fasoriales para encontrar el Fasor Resultante mediante la ley del paralelogramo.

Ejemplo de Suma de Fasores

Solución:

El voltaje total (\(V_T\)) se puede encontrar dibujando un diagrama fasorial y construyendo un paralelogramo. Los dos lados son \(V_1\) y \(V_2\).

El método gráfico (midiendo la diagonal) puede tener errores. Por eso, usamos un método analítico: la forma rectangular.

En forma rectangular, el fasor se divide en una parte real (x) y una parte imaginaria (y), formando la expresión \( Z = x \pm jy \). La suma de dos vectores A y B es:

\[ V_A = V_{Ax} + jV_{Ay} \]\[ V_B = V_{Bx} + jV_{By} \]\[ V_T = (V_{Ax} + V_{Bx}) + j(V_{Ay} + V_{By}) \]

Suma de fasores usando forma rectangular

Usaremos \(V_2\) como nuestra referencia, colocándolo en el eje horizontal (ángulo 0°).

1. Descomponer V2 (Referencia)El voltaje \(V_2\) (30V) apunta a 0°. No tiene componente vertical.

   \[ V_{2x} = 30 \cos(0^\circ) = 30 V \]\[ V_{2y} = 30 \sin(0^\circ) = 0 V \]

   Expresión rectangular para \(V_2\): \( 30 + j0 \)

2. Descomponer V1El voltaje \(V_1\) (20V) adelanta a \(V_2\) por 60°.

   \[ V_{1x} = 20 \cos(60^\circ) = 10 V \]\[ V_{1y} = 20 \sin(60^\circ) = 17.32 V \]

   Expresión rectangular para \(V_1\): \( 10 + j17.32 \)

3. Sumar componentesSumamos las partes reales (horizontales) e imaginarias (verticales).

   \[ V_{\text{horizontal}} = V_{1x} + V_{2x} = 10 + 30 = 40 V \]\[ V_{\text{vertical}} = V_{1y} + V_{2y} = 17.32 + 0 = 17.32 V \]

   El fasor resultante \(V_T\) es: \( 40 + j17.32 \)

4. Calcular Magnitud (Teorema de Pitágoras)Ahora que tenemos los dos catetos del triángulo (real e imaginario), encontramos la hipotenusa (magnitud).

   \[ V_{T} = \sqrt{V_{\text{horizontal}}^2 + V_{\text{vertical}}^2} \]\[ V_{T} = \sqrt{(40)^2 + (17.32)^2} \]\[ V_{T} = \sqrt{1600 + 299.98} = \sqrt{1899.98} \]\[ V_{T} \approx 43.6 V \]

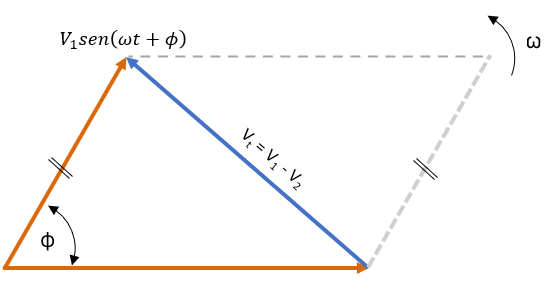
Sustracción fasorial de diagramas fasoriales

La resta es muy similar, pero se toma la otra diagonal del paralelogramo. En forma rectangular, simplemente restamos los componentes.

\[ V_A = V_{Ax} + jV_{Ay} \]\[ V_B = V_{Bx} + jV_{By} \]\[ V_{\text{Resta}} (A-B) = (V_{Ax} - V_{Bx}) + j(V_{Ay} - V_{By}) \]

Los diagramas fasoriales trifásicos ⚡️

Hasta ahora vimos sistemas monofásicos. Si tres bobinas idénticas se colocan a 120° eléctricos entre sí en el mismo rotor, se genera un suministro de voltaje trifásico.

Un suministro trifásico balanceado consta de tres voltajes sinusoidales iguales en magnitud y frecuencia, pero desfasados 120° entre sí.

La práctica estándar es codificar las fases: Rojo (R), Amarillo (Y) y Azul (B). La secuencia normal de rotación es R-Y-B. Los fasores giran en sentido antihorario (\(\omega\)).

Los voltajes de fase son iguales en magnitud, difiriendo solo en el ángulo. Si la fase Roja se toma como referencia (RN), cada voltaje de fase se puede definir respecto al neutro común.

Fórmulas de voltaje trifásico

Si \(V_{RN}\) (fase Roja) es la referencia:

\[ V_{RN} = V_p \sin(\omega t) \]\[ V_{YN} = V_p \sin(\omega t - 120^\circ) \]\[ V_{BN} = V_p \sin(\omega t - 240^\circ) \text{ o } V_p \sin(\omega t + 120^\circ) \]

El voltaje en la fase Amarilla se retrasa 120° de la Roja, y el voltaje en la Azul se retrasa 120° de la Amarilla. También podemos decir que el Azul se "adelanta" 120° al Rojo.

Como los tres voltajes están "equilibrados" (misma magnitud, desfase de 120°), en un sistema trifásico balanceado, la suma fasorial de los voltajes de fase es siempre cero: \( V_R + V_Y + V_B = 0 \).