Impedancia en Corriente Alterna

La impedancia es conocida como la oposición al flujo de corriente en un circuito de corriente alterna, así como también en un circuito de corriente continua donde la oposición al flujo de corriente se le llama “resistencia”. Al igual que la impedancia esta es medida en ohmios.

Hasta este punto hemos visto que en un circuito de corriente alterna que contiene formas de ondas sinusoidales, se pueden usar fasores de voltaje y corriente junto con números complejos para representar una cantidad compleja.

También vimos que las formas de onda sinusoidales y las funciones que se dibujaron previamente en la transformación del dominio del tiempo se pueden convertir en el dominio fasorial para que los diagramas fasoriales se puedan construir para encontrar esta relación voltaje-corriente fasorial.

Ahora que sabemos cómo representar un voltaje o una corriente como un fasor, podemos ver esta relación cuando se aplica a elementos de circuitos pasivos básicos, como una resistencia de CA cuando se conecta a un suministro de CA monofásico.

Cualquier elemento de circuito básico ideal, como una resistencia, se puede describir matemáticamente en términos de su voltaje y corriente, recordemos también que las resistencias óhmicas son linealmente proporcionales a la corriente que fluye a través de ella, según lo definido por la Ley de Ohm. (veamos el siguiente circuito)

Cuando el interruptor está cerrado, se aplica una tensión de CA, V, a la resistencia, R. Esta tensión hará que fluya una corriente que, a su vez, subirá y bajará a medida que la tensión aplicada suba y baje sinusoidalmente. Como la carga es una resistencia, la corriente y la tensión alcanzarán sus valores máximos o de pico y caerán hasta el cero exactamente al mismo tiempo, es decir, subirán y bajarán simultáneamente y, por tanto, se dice que están "en fase".

Entonces la corriente eléctrica que fluye a través de una resistencia de CA varía sinusoidalmente con el tiempo y se representa por la expresión, I(t) = Im x sin(ωt + θ), donde Im es la amplitud máxima de la corriente y θ es su ángulo de fase. Además, también podemos decir que para cualquier corriente dada, i que fluye a través de la resistencia el voltaje máximo o de pico a través de los terminales de R estará dado por la Ley de Ohm como:

$\displaystyle {{V}_{{(t)}}}=R{{I}_{{(t)}}}=R{{I}_{m}}sen\left( {\omega t+\theta } \right)$

y el valor instantáneo de la corriente, será:

$\displaystyle {{i}_{{R(t)}}}={{I}_{{R\left( {\max } \right)}}}sen\omega t$

Así, para un circuito puramente resistivo, la corriente alterna que fluye a través de la resistencia varía en proporción a la tensión aplicada a través de ella siguiendo el mismo patrón sinusoidal. Como la frecuencia de alimentación es común a la tensión y a la corriente, sus fasores también serán comunes, por lo que la corriente estará "en fase" con la tensión, ( θ = 0 ).

En otras palabras, no hay diferencia de fase entre la corriente y la tensión cuando se utiliza una resistencia de CA, ya que la corriente alcanzará sus valores máximos, mínimo y cero siempre que la tensión alcance sus valores máximos, mínimo y cero, como se muestra a continuación.

Forma de Onda Sinusoidal para la resisténcia de CA

Este efecto "en fase" también puede representarse mediante un diagrama fasorial. En el dominio complejo, la resistencia es un número real, lo que significa que no hay componente "j" o imaginario. Por lo tanto, como la tensión y la corriente están ambas en fase entre sí, no habrá diferencia de fase ( θ = 0 ) entre ellas, por lo que los vectores de cada cantidad se dibujan superpuestos uno sobre otro a lo largo del mismo eje de referencia. La transformación del dominio temporal sinusoidal al dominio fasorial viene dada por.

Diagrama de fasores para la resistencia de CA

Como un fasor representa los valores eficaces de las magnitudes de tensión y corriente, a diferencia de un vector que representa los valores máximos o de cresta, dividiendo el valor de cresta de las expresiones en el dominio del tiempo anteriores por √2, la relación correspondiente entre el fasor de tensión y el de corriente se da como.

Relación RMS

Relación de Fase

Esto muestra que una resistencia pura dentro de un circuito de CA produce una relación entre sus fasores de tensión y corriente exactamente de la misma manera que relacionaría la misma relación de tensión y corriente de las resistencias dentro de un circuito de CC. Sin embargo, en un circuito de CC esta relación se denomina comúnmente Resistencia, tal como se define en la Ley de Ohm, pero en un circuito de CA sinusoidal esta relación tensión-corriente se denomina ahora Impedancia. En otras palabras, en un circuito de CA la resistencia eléctrica se llama "Impedancia".

En ambos casos esta relación tensión-corriente ( V-I ) es siempre lineal en una resistencia pura. Por lo tanto, cuando se utilizan resistencias en circuitos de CA, el término Impedancia, símbolo Z, es el que se utiliza generalmente para significar su resistencia. Por lo tanto, podemos decir correctamente que para una resistencia, la resistencia CC = impedancia CA , o R = Z.

El vector impedancia se representa con la letra, ( Z ) para un valor de resistencia CA con las unidades de Ohm ( Ω ) igual que para CC. Entonces la Impedancia ( o resistencia CA ) se puede definir como:

Impedancia de Corriente Alterna

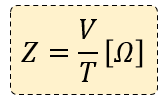
La impedancia también puede representarse mediante un número complejo, ya que depende de la frecuencia del circuito, ω cuando hay componentes reactivos. Pero en el caso de un circuito puramente resistivo esta componente reactiva será siempre cero y la expresión general para la impedancia en un circuito puramente resistivo dada como un número complejo será:

Dado que el ángulo de fase entre la tensión y la corriente en un circuito de CA puramente resistivo es cero, el factor de potencia también debe ser cero y viene dado por: cos 0° = 1, Entonces la potencia instantánea consumida en la resistencia viene dada por:

Sin embargo, como la potencia media en un circuito resistivo o reactivo depende del ángulo de fase y en un circuito puramente resistivo éste es igual a θ = 0, el factor de potencia es igual a uno por lo que la potencia media consumida por una resistencia de CA puede definirse simplemente utilizando la Ley de Ohm como:

$\displaystyle P=VI={{I}^{2}}R=\frac{{{{V}^{2}}}}{R}$

que son las mismas ecuaciones de la Ley de Ohm que para los circuitos de CC. Entonces la potencia efectiva consumida por una resistencia de CA es igual a la potencia consumida por la misma resistencia en un circuito de CC.

Muchos circuitos de CA, como los elementos de calefacción y las lámparas, están formados únicamente por una resistencia óhmica pura y tienen valores insignificantes de inductancia o capacitancia que contienen impedancia.

En estos circuitos podemos utilizar tanto la Ley de Ohm como la Ley de Kirchoff, así como simples reglas de circuito para calcular y encontrar la tensión, la corriente, la impedancia y la potencia como en el análisis de circuitos de CC. Cuando se trabaja con estas reglas es habitual utilizar sólo los valores RMS.

Ejemplos Resueltos de Impedancia

Solución: Obtenemos primeramente la corriente del suministro mediante la ley del Ohm:

$\displaystyle I=\frac{V}{R}=\frac{{240}}{{60}}=4A$

Obteniendo como resultado 4 Amperes

Ahora obtenemos la potencia actia consumida por la resistencia de CA, realizando lo siguiente:

$\displaystyle P={{I}^{2}}R={{\left( 4 \right)}^{2}}\left( {60} \right)=(16)(60)=960W$

obteniendo 960 Watts

Ahora como no hay diferencia de fase en un componente resistivo, donde ( θ = 0 ), el diagrama fasorial correspondiente se da como:

Solución: El voltaje sinusoidal a través de la resistencia será el misom que para el suministro en un circuito puramente resistivo. Convertir este voltaje de la expresión en el dominio del tiempo a la expresión en el dominio del fasor nos da

$\displaystyle {{V}_{{R(t)}}}=100\cos \left( {\omega t+30{}^\circ } \right)$

al dominio del fasor:

$\displaystyle {{V}_{R}}=100\angle 30{}^\circ $

Aplicando la ley del Ohm nos da:

$\displaystyle {{I}_{R}}=\frac{{100\angle 30{}^\circ }}{{50\Omega }}=2\angle 30{}^\circ A$

El diagrama fasorial correspondiente será por tanto:

Resumen de la impedancia

En una resistencia óhmica pura de CA, la corriente y el voltaje están ambas "en fase", ya que no hay diferencia de fase entre ellas. La corriente que fluye a través de la resistencia es directamente proporcional a la tensión que la atraviesa, y esta relación lineal en un circuito de CA se denomina Impedancia.

La impedancia, a la que se le da la letra Z, en una resistencia óhmica pura es un número complejo que consta sólo de una parte real que es el valor real de la resistencia de CA, ( R ) y una parte imaginaria cero, ( j0 ). Debido a esto la Ley de Ohm puede ser usada en circuitos que contienen una resistencia de CA para calcular estos voltajes y corrientes.