Conversión Delta-Estrella y Estrella-Delta

¿Qué tal lectores?, hoy hablaremos sobre un tema muy importante en el análisis de circuitos y se trata sobre las configuraciones delta-estrella, o viceversa estrella-delta, éstas configuraciones de circuito son realizadas en los resistores que no tienen la forma de serie o paralelo, así también es imposible hacer una análisis detallado con el método de mallas o el método de nodos, sin embargo veremos unas formas muy sencillas de convertir de una manera a otra. 😎

Si bien hay formas de llamar a la configuración estrella como Y o T, y la configuración delta como pi, entonces las ilustremos para que sea de mejor entendimiento.

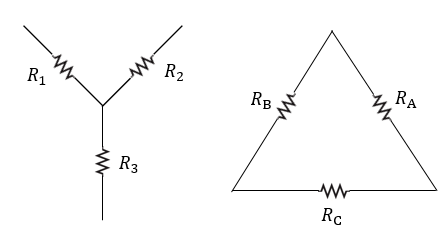
Por lo general, obtendríamos un resultado similar al siguiente al momento de realizar nuestra conversión matemática de una forma a otra, pero nada complicado:

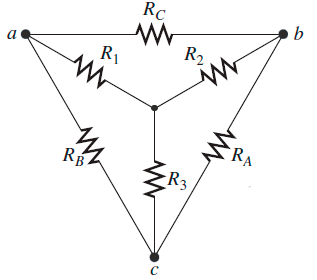
¿Cómo es la configuración delta (Δ) ?

Antes de comenzar a ver las fórmulas empleadas en este artículo, es importante que sepamos que en un circuito delta, los tres componentes del sistema (generalmente resistencias, impedancias o bobinas) están conectados en un bucle cerrado formando un triángulo. Cada vértice del triángulo está conectado a una fase de la fuente de alimentación.

• Característica clave: Las corrientes de línea (aquellas que circulan entre la fuente de alimentación y los vértices del triángulo) no son iguales a las corrientes de fase (aquellas que circulan por los componentes del triángulo). De hecho, la corriente de línea es mayor que la corriente de fase.

¿Cómo es la configuración estrella (Y) ?

En este tipo de la configuración estrella, un extremo de cada componente está conectado a un punto común o "neutro", mientras que los otros extremos están conectados a cada una de las fases de la fuente de alimentación.

• Característica clave: En la configuración estrella, las tensiones de fase son menores que las tensiones de línea. La corriente de línea es la misma que la corriente de fase.

Aplicaciones en la vida real

• Transformadores: En sistemas de distribución eléctrica, es común que los transformadores utilicen estas configuraciones para ajustar las tensiones y corrientes en diferentes puntos de una red.
• Motores trifásicos: Muchos motores industriales cambian entre conexiones delta y estrella para gestionar el arranque y el funcionamiento.

Conversión de Delta a Estrella

La demostración de ésta fórmula es muy sencilla, por ejemplo sabemos que la configuración delta contiene las siguientes resistencias:

$\displaystyle {{R}_{A}},{{R}_{B}},{{R}_{C}}$

Y la configuración estrella, contiene éstas otras:

$\displaystyle {{R}_{1}},{{R}_{2}},{{R}_{3}}$

Pues bien, para pasar de Delta a Estrella, lo haremos de la siguiente manera, prestar atención a lo único que hay que tomar importancia.

1. El valor de la resistencia que se desea conocer, se multiplica por las resistencias de sus costados.
2. El resultado del producto de las resistencias del costado, se divide entre la suma de todas las resistencias.

Obteniendo R1

Siguiendo este pequeño algoritmo, podemos establecer entonces que si deseamos conocer el valor de la resistencia R1, buscamos las dos resistencias de sus costados que son Rb y Rc, y la dividimos por la suma de todas las resistencias es decir Ra + Rb + Rc.

¿fácil no? , entonces esto quedaría de la siguiente forma.

$\displaystyle {{R}_{1}}=\frac{{{R}_{B}}{{R}_{C}}}{{{R}_{A}}+{{R}_{B}}+{{R}_{C}}}$

Obteniendo R2

Hacemos el mismo procedimiento, es decir buscamos a R2 y vemos que resistencias están a su costado, en este caso es Ra y Rc, entonces sabemos que a ese producto lo vamos a dividir por la suma total, entonces tendríamos lo siguiente.

$\displaystyle {{R}_{2}}=\frac{{{R}_{A}}{{R}_{C}}}{{{R}_{A}}+{{R}_{B}}+{{R}_{C}}}$

Obteniendo R3

Si seguimos el procedimiento, es fácil inferir, quiénes serán las dos resistencias que se multiplicarán en la parte del numerador, pues el denominador sabemos que es la suma de las tres resistencias en total. Entonces decimos que las únicas resistencias para R3 es Ra y Rb.

$\displaystyle {{R}_{3}}=\frac{{{R}_{A}}{{R}_{B}}}{{{R}_{A}}+{{R}_{B}}+{{R}_{C}}}$

Conversión de Estrella a Delta

Ahora es momento de observar como es posible obtener Ra, Rb, y Rc, la verdad no es difícil, pero si es importante tener en cuenta los siguientes dos puntos:

1. El numerador estará fijo para las conversiones, y es muy fácil obtenerlo, solamente debemos multiplicar R1 con R2, luego sumar R1 con R3 y finalmente sumar R2 con R3, el resultado del producto de las resistencias.
2. Se dividirá con la resistencia que es opuesta a la resistencia que deseamos convertir.

Obteniendo Ra

Siguiendo el algoritmo tendremos entonces que:

$\displaystyle {{R}_{A}}=\frac{{{R}_{1}}{{R}_{2}}+{{R}_{1}}{{R}_{3}}+{{R}_{2}}{{R}_{3}}}{{{R}_{1}}}$

El R1 abajo, es porque es la resistencia opuesta a la resistencia Ra

Obteniendo Rb

Hacemos lo mismo del paso uno, lo que más nos interesa saber es ver con que resistencia opuesta está relacionada, a simple hecho vemos que esa resistencia es R2. Entonces nuestra fórmula sería:

$\displaystyle {{R}_{B}}=\frac{{{R}_{1}}{{R}_{2}}+{{R}_{1}}{{R}_{3}}+{{R}_{2}}{{R}_{3}}}{{{R}_{2}}}$

Obteniendo Rc

Ya sabemos como es el algoritmo, entonces podemos inferir que para encontrar Rc, tendríamos que aplicar la siguiente fórmula.

$\displaystyle {{R}_{C}}=\frac{{{R}_{1}}{{R}_{2}}+{{R}_{1}}{{R}_{3}}+{{R}_{2}}{{R}_{3}}}{{{R}_{3}}}$

📃 Conversión de Delta a Estrella Ejercicios Resueltos

Vemos entonces, si hemos captado el tipo de configuración de un sistema a otro, para ello veamos el siguiente ejemplo. 👇

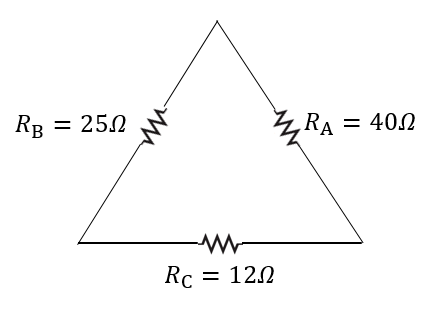
Solución: 

Recordemos la operación para obtener el valor de R1, R2 y R3.

Pero para entenderlo mejor, hagamos un bosquejo, de como serán los resultado al hacer las configuraciones.

Aplicando las fórmulas correspondientes, tenemos entonces que:

Para R1:

$\displaystyle {{R}_{1}}=\frac{{{R}_{B}}{{R}_{C}}}{{{R}_{A}}+{{R}_{B}}+{{R}_{C}}}=\frac{(25\Omega )(12\Omega )}{25\Omega +40\Omega +12\Omega }=\frac{300{{\Omega }^{2}}}{77\Omega }=3.896\Omega $

Para R2:

$\displaystyle {{R}_{2}}=\frac{{{R}_{A}}{{R}_{C}}}{{{R}_{A}}+{{R}_{B}}+{{R}_{C}}}=\frac{(40\Omega )(12\Omega )}{77\Omega }=\frac{480{{\Omega }^{2}}}{77\Omega }=6.234\Omega $

Para R3:

$\displaystyle {{R}_{3}}=\frac{{{R}_{A}}{{R}_{B}}}{{{R}_{A}}+{{R}_{B}}+{{R}_{C}}}=\frac{(40\Omega )(25\Omega )}{77\Omega }=\frac{1000{{\Omega }^{2}}}{77\Omega }=12.987\Omega $

Qué sería nuestra nueva conversión y habríamos resuelto el sistema de delta a estrella.

Ahora veamos el mismo procedimiento, pero al revés. Es decir, hagamos una conversión estrella a delta.

Solución:

En algunas ocasiones, los ejercicios de delta-estrella puede referirse a situaciones donde todas las resistencias son iguales, entonces en ese proceso aplicaremos:

$\displaystyle {{R}_{Y}}=\frac{{{{R}_{\Delta }}}}{3}$

Entonces:

$\displaystyle {{R}_{Y}}=\frac{{18}}{3}=6\Omega $

Por lo que 6Ω sería la respuesta correcta.

💡 Conversión de Estrella a Delta Ejercicios Resueltos

Para iniciar un ejercicio sobre la conversión de estrella a delta, vamos a considerar el siguiente ejemplo:

Solución: 

Sabemos que podemos trazarlo como el ejemplo anterior, para ver como establecer nuestra fórmula, entonces procedamos a realizar un bosquejo.

Aplicando nuestras fórmulas establecidas:

Para RA:

$\displaystyle {{R}_{A}}=\frac{(50\Omega )(50\Omega )+(50\Omega )(50\Omega )+(50\Omega )(50\Omega )}{50\Omega }=150\Omega $

De aquí podemos observar que como se tratan de resistencias iguales, es lógico que las demás nos proporcionen el mismo valor.

Para RB:

$\displaystyle {{R}_{B}}=\frac{7500{{\Omega }^{2}}}{50\Omega }=150\Omega $

Para RC:

$\displaystyle {{R}_{B}}=\frac{7500{{\Omega }^{2}}}{50\Omega }=150\Omega $

Solución:

El mismo problema que la situación anterior, donde las resistencias son iguales. Cuando esto sucede, el procedimiento es mucho más fácil para su resolución.

Entonces, aplicamos:

$\displaystyle {{R}_{\Delta }}=3{{R}_{Y}}$

Sustituyendo

$\displaystyle {{R}_{\Delta }}=3\left( {10\Omega } \right)=30\Omega $

Qué sería la nueva configuración.

Con estos cuatro ejemplos, podemos aprender mucho sobre la base de las conversiones delta - estrella.

Análisis de potencia en configuración delta-estrella

Veamos un problema del tipo de análisis de potencia.

Solución:

Calculando la potencia en configuración delta.

$\displaystyle {{I}_{L}}=\frac{{{{V}_{L}}}}{{{{R}_{\Delta }}}}=\frac{{400}}{{15}}\approx 26.67A$

La potencia total en delta es:

$\displaystyle {{P}_{\Delta }}=3\times {{V}_{L}}\times {{I}_{L}}=3\times 400\times 26.67\approx 32,004W$

Conversión a estrella:

Convirtiendo las resistencias a estrella:

$\displaystyle {{R}_{Y}}=\frac{{R\Delta }}{3}=\frac{{15}}{3}=5\Omega $

La corriente de línea en estrella es:

$\displaystyle {{I}_{L}}=\frac{{{{V}_{L}}}}{{\sqrt{3}\times {{R}_{Y}}}}=\frac{{400}}{{\sqrt{3}\times 5}}\approx 46.19A$

La potencia total en estrella es:

$\displaystyle {{P}_{Y}}=3\times {{V}_{L}}\times {{I}_{L}}=3\times 400\times 46.19\approx 55,428W$

Qué sería la respuesta al problema.

Errores más comunes y a tomar en cuenta

Los errores más comunes al realizar la conversión delta-estrella suelen estar relacionados con la comprensión incorrecta de las relaciones entre corrientes, tensiones, o la mala aplicación de las fórmulas. Aquí hemos detallado las más frecuentes:

1. Confusión entre tensiones y corrientes de fase y de línea

• Error: Confundir las tensiones y corrientes de fase con las de línea al realizar las conversiones.
• Explicación: En la configuración estrella, la tensión de fase es menor que la tensión de línea por un factor de √3, mientras que en delta la tensión de fase y la tensión de línea son iguales. Lo mismo sucede con las corrientes, pero al revés: en estrella las corrientes de línea son iguales a las de fase, mientras que en delta las corrientes de línea son √3 veces mayores que las de fase. No tener en cuenta esta diferencia al realizar cálculos puede llevar a errores graves en la selección de componentes o dimensionamiento del sistema.

2. Uso incorrecto de las fórmulas de conversión

• Error: Aplicar incorrectamente las fórmulas para convertir entre delta y estrella.
• Explicación: Las fórmulas para la conversión de delta a estrella y de estrella a delta son diferentes. No tener claro qué configuración estás manejando o usar las fórmulas en el orden incorrecto puede llevar a cálculos erróneos. Recordar que:
  • Para convertir de delta a estrella: $\displaystyle {{R}_{y}}=\frac{{{{R}_{\Delta }}}}{3}$​
  • Para convertir de estrella a delta: $\displaystyle {{R}_{\Delta }}=3\times {{R}_{y}}$​

3. Desbalance en las impedancias

• Error: No tomar en cuenta el balance entre impedancias en las tres fases.
• Explicación: En un sistema trifásico equilibrado, las tres impedancias (resistencias o reactancias) deben ser iguales. Si al convertir entre delta y estrella las impedancias no se mantienen equilibradas, se puede producir un desbalance en el sistema, generando sobrecalentamiento o funcionamiento ineficiente. Este error es común cuando se utilizan componentes de diferente valor para cada fase.

4. Ignorar el efecto del punto neutro en estrella

• Error: No tener en cuenta que la configuración estrella tiene un punto neutro que puede ser necesario conectar a tierra.
• Explicación: En estrella, el punto neutro es crucial para estabilizar el sistema y proporcionar un camino de retorno para las corrientes de desequilibrio. Si este punto neutro no está correctamente conectado, el sistema puede sufrir desequilibrios de tensión y sobrecargas en las fases.

5. Incorrecta interpretación del diagrama de conexiones

• Error: Conectar mal los componentes al no entender adecuadamente los diagramas de las configuraciones delta y estrella.
• Explicación: Un error muy común es conectar erróneamente las fases en la configuración delta, donde cada componente debe estar conectado entre dos fases, o en la configuración estrella, donde cada componente debe estar conectado entre una fase y el neutro. Conexiones incorrectas pueden resultar en cortocircuitos o en que el sistema no funcione como se espera.

6. No considerar la potencia total del sistema

• Error: Suponer que la potencia total cambia al convertir entre configuraciones.
• Explicación: La potencia total en un sistema trifásico no cambia al convertir entre delta y estrella. Lo que cambia es cómo se distribuyen las corrientes y tensiones, pero la potencia debe permanecer constante. Algunos errores ocurren cuando se recalculan los valores de potencia sin tener esto en cuenta.

7. Selección inadecuada de componentes

• Error: No seleccionar correctamente las resistencias, inductancias o capacitancias necesarias para cada configuración.
• Explicación: Los componentes que son adecuados para una configuración delta pueden no serlo para una configuración estrella, debido a las diferencias en tensiones y corrientes. Esto puede llevar a sobrecalentamientos o fallos en los equipos si los componentes no están dimensionados correctamente para la nueva configuración.

8. No tener en cuenta las diferencias en protección

• Error: No ajustar los sistemas de protección (fusibles, disyuntores) al cambiar de una configuración a otra.
• Explicación: Las configuraciones delta y estrella pueden requerir diferentes valores de protección debido a las diferencias en las corrientes de línea y de fase. No realizar los ajustes necesarios en los sistemas de protección puede llevar a que estos no funcionen correctamente o que se dañen los equipos.

Evitar estos errores requiere una comprensión clara de las características de cada configuración y una atención cuidadosa a los cálculos y conexiones.